Banana plots

Before calculating an exposure age or erosion rate, it is a good idea to check if the TCN measurements are consistent with a simple or complex exposure history. This can be done with two nuclides (including at least one radionuclide) using a ``banana plot'' (Lal, 1991). CosmoCalc accomodates two types of banana plot: $^{26}$Al-$^{10}$Be and $^{21}$Ne-$^{10}$Be. Depending on whether or not a sample plots above, below or inside the so-called ``steady-state erosion island'' (Lal, 1991), one can decide whether or not to pursue the calculation of an exposure age, erosion rate or burial age. For the construction of the banana plots and the age/erosion calculations of Section 5, CosmoCalc implements a modified version of the ingrowth equation of Granger and Muzikar (2001):

$$N = P e^{- \lambda \tau} \sum_{i=0}^3 \frac{F_i}{\lambda + \eps... ... \left( 1 - e^{- \left( \lambda + \epsilon \rho / \Lambda_i \right) t} \right)$$ (4)

With N the nuclide concentration (atoms/g), P the total surface production rate (in atoms/g/yr) at SLHL, $\tau$ the burial age, $\epsilon$ the erosion rate, t the exposure age and $\lambda$ the radioactive half-life of the nuclide. Equation 4 models TCN production by neutrons, slow and fast muons by a series of exponential approximations. The first term of the summation models TCN production by spallogenic neutron reactions, the second and third terms model slow muons and the last term approximates TCN production by fast muons. Thus, $F_0,...,F_3$ are dimensionless numbers between zero and one, and $\Lambda_0,...,\Lambda_3$ are attenuation lengths (g/cm$^2$). The approach of Granger et al. (2000, 2001) was chosen because of its flexibility. For instance, neglecting muon production can be easily implemented by setting $F_1,F_2$ and $F_3$ equal to zero in Equation 4. CosmoCalc uses Granger et al.'s (2000, 2001) recommended values of $F_0,...,F_3$ for $^{10}$Be and $^{26}$Al, but also offers an alternative choice of pre-set values approximating either the alternative parameterization of Schaller et al. (2001), neglecting the contribution of muons, or only using three exponentials (for more details, see Section 7). Banana plots with non-zero muon contributions feature a characteristic cross-over of the steady-state and zero erosion lines which is absent when muons are neglected (Figure 2).

CosmoCalc's banana plots are normalized to SLHL, meaning that the TCN concentrations of each sample are divided by the cumulative effect of all their correction factors, represented by the ``effective scaling factor'' $S_e$:

$$S_e = S_t \times f(S)$$ (5)

with

$$S = S_p \times S_s \times S_c$$ (6)

where $S_p$ is one of the production rate scaling factors of Section 2 and $S_t$, $S_s$ and $S_c$ are defined in Section 3. If muon production is neglected, then $S_e$ = $S_t \times S_p \times S_s \times S_c$. However, in the presence of muons, the effective scaling factor $S_e$ may deviate from this value because the relative importance of the different production mechanisms changes as a function of age, erosion rate, elevation, latitude, sample thickness and snow cover. The exact form of the function f(S) will be defined in Section 5. Note that the topographic shielding correction $S_t$ does not ``fractionate'' (i.e., change the fractions $F_0$,...,$F_3$ of) the different production mechanisms and is placed outside the scaling function f(S). This means that, strictly speaking, the TCN concentrations should be multiplied by $S_t$ prior to generating a banana plot. The input required by CosmoCalc's ``Banana'' function are (1) the composite scaling factor S for the first nuclide ($^{26}$Al or $^{21}$Ne), (2) the concentration and 1$\sigma$ measurement uncertainty of the first nuclide ($^{26}$Al or $^{21}$Ne), both multiplied by $S_t$, (3) S for the second nuclide ($^{10}$Be) and (4) the concentration and 1$\sigma$ measurement uncertainty of the second nuclide ($^{10}$Be), also multiplied by $S_t$. Because topographic shielding corrections are generally small, the systematic error caused by lumping $S_t$ together with the other correction factors is very small. Therefore, if $S_t > \sim$ 0.95, say, it is safe to approximate Equation 5 by $S_e$ = f( $S_t \times S_p \times S_s \times S_c$). In this case, the nuclide concentrations do not need to be pre-multiplied by $S_t$.

Figure 2: By using the TCN production equation of Granger et al. (2000, 2001; Equation 4), CosmoCalc's banana-plots are very flexible. Two examples of $^{21}$Ne/$^{10}$Be-banana plots illustrate this flexibility: a. with default parameters as given by Granger and Smith (2000) and in Table 1; b. using only spallation by neutrons, i.e. no muons. TCN production by muons causes a characteristic cross-over of the zero-erosion and infinite exposure lines at low $^{10}$Be concentrations. The ellipses mark the 2$\sigma$ uncertainties of three samples (labeled a, b and c).

a.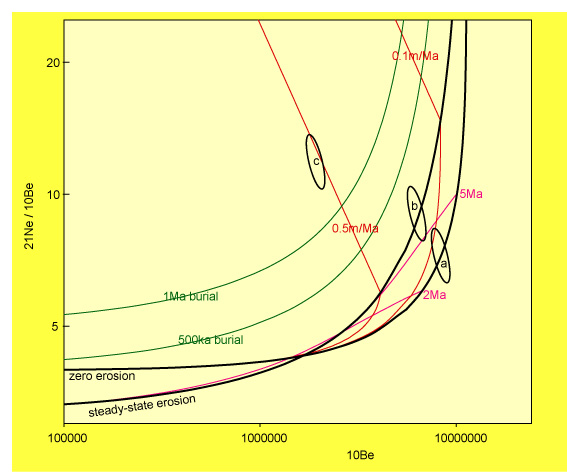
b.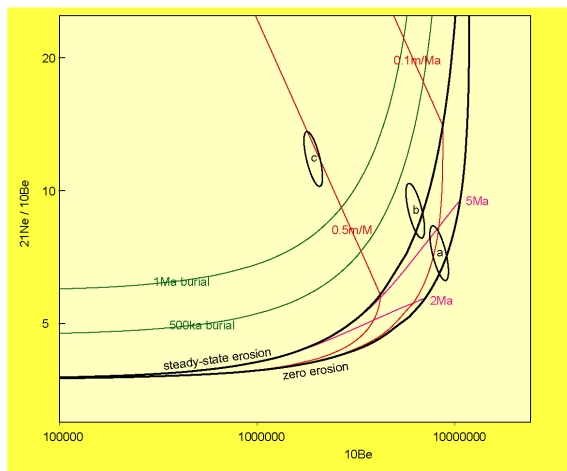

The graphical output of CosmoCalc can easily be copied and pasted for editing in vector graphics software such as Adobe Illustrator or CorelDraw. The y-axis of the $^{26}$Al-$^{10}$Be plot is logarithmic by default whereas the y-axis of the $^{21}$Ne-$^{10}$Be plot is linear. These defaults can be changed in the ``Banana Options'' userform. Note that MS-Excel (versions 2000 and 2003) only allows logarithmic tickmarks to have values in multiples of ten. To get around this limitation, CosmoCalc uses a ``pseudo y-axis'', which cannot be edited by the usual right mousebutton-click. Hopefully, this limitation will not be necessary in later versions of Excel. CosmoCalc only propagates the analytical uncertainty of the measured TCN concentrations. No uncertainty is assigned to the production rate scaling factors, radioactive half-lives or other potentially ill-constrained quantities. On the banana plots, the user is offered the choice between error bars or -ellipses with the latter being the default. Banana plots are graphs of the type $N_1$/$N_2$ vs. $N_2$ which are always associated with some degree of ``spurious correlation'' (Chayes, 1949). This causes the error ellipses to be rotated according to the following correlation coefficient:

$$\rho_c = - \frac{\overline{N}_1 \sigma_{N_2} } { \sqrt{\overline{N}_2^2 \sigma_{N_1}^2 + \overline{N}_1^2 \sigma_{N_2}^2}}$$ (7)

If $N_1$ stands for $^{26}$Al or $^{21}$Ne and $N_2$ for $^{10}$Be, then $\overline{N}_1$ and $\overline{N}_2$ are the measured concentrations of these respective nuclides while $\sigma_{N_1}$ and $\sigma_{N_2}$ are the corresponding measurement uncertainties.