Age/erosion rate calculations

Equation 4 has three unknowns: t (exposure age), $\epsilon$ (erosion rate) and $\tau$ (burial age). If only one nuclide was measured, we must assume values for two of these quantities in order to solve for the third. If two nuclides were analysed (of which at least one is radioactive), only one assumption is needed. CosmoCalc is capable of both approaches. In this section, we will first discuss how to solve for $\epsilon$ (assuming infinite exposure age and zero burial) and t (assuming zero erosion and burial) using a single nuclide (Section 5). Then, numerical methods will be presented to simultaneously solve for t and $\epsilon$ (assuming zero burial), t and $\tau$ (assuming zero erosion) or $\epsilon$ and $\tau$ (assuming infinite exposure age), using two nuclides (Section 5). Note that in the case of two nuclides ($^{26}$Al or $^{21}$Ne combined with $^{10}$Be), the assumption of zero burial can be verified on the banana plot.

Calculations using a single nuclide

CosmoCalc requires three pieces of information to calculate an exposure age or erosion rate: the TCN concentration (corrected for topography), its analytical uncertainty and a composite correction factor for production rate scaling with latitude/elevation and shielding (Equation 6). We somehow need to incorporate this scaling factor into the ingrowth equation (Equation 4). This poses a problem because the scaling factor is a single number whereas Equation 4 explicitly makes the distinction between neutrons, slow and fast muons. Granger and Smith (2000) avoid this problem by separately scaling the different production mechanisms:

$$N(t,\epsilon,\tau) = P e^{- \lambda \tau} \sum_{i=0}^3 \frac{S_... ... \left( 1 - e^{- \left( \lambda + \epsilon \rho / \Lambda_i \right) t} \right)$$ (8)

Instead of one scaling factor, Equation 8 has four, one for neutrons ($S_0$), two for slow muons ($S_1$ and $S_2$) and one for fast muons ($S_3$). Granger et al. (2001) separately calculate each of these four scaling factors. Thus, the original method of Granger and Smith (2000) is incompatible with the common practice of lumping all production mechanisms into a single latitude/elevation scaling factor (Section 2). To ensure optimal flexibility and user-friendliness, CosmoCalc uses a slightly different approach. $S_0,...,S_3$ are calculated from the composite correction factor S, by approximating the total scaling by a single attenuation factor caused by a virtual layer of matter of thickness x (in g/cm$^2$):

$$S_i = e^{-x/\Lambda_i}$$ (9)

so that

$$\sum_{i=0}^3 S_i F_i = S$$ (10)

with $F_i$ and $\Lambda_i$ as in Equation 4 and S as defined in Equation 6. CosmoCalc solves Equation 10 iteratively using Newton's method.

As said before, some assumptions are needed to solve Equation 8. An exposure age (t) can be calculated under the assumption of zero erosion and burial ($\epsilon$ = 0, $\tau$ = 0). For a radionuclide with decay constant $\lambda$, this yields:

$$t = - \frac{1}{\lambda} ln\left(1 - \frac{N \lambda}{P S}\right)$$ (11)

whereas for stable nuclides ($^3$He and $^{21}$Ne):

$$t = \frac{N}{P S}$$ (12)

Alternatively, the erosion rate ($\epsilon$) can be calculated under the assumption of steady state and zero burial (t = $\infty$, $\tau$=0):

$$N(\epsilon) = P \sum_{i=0}^3 \frac{S_i F_i}{\lambda + \epsilon \rho / \Lambda_i}$$ (13)

CosmoCalc solves this equation iteratively using Newton's method. Statistical uncertainties are estimated by standard error propagation:

$$\sigma_t = \frac{\sigma_N}{P S - N \lambda}$$ (14)

$$\sigma_{\epsilon} = \frac{\sigma_N} {P \sum_{i=0}^3 \frac{S_i F_i} {\left( (\Lambda_i / \rho) (\lambda + \epsilon \rho / \Lambda_i)\right)^2}}$$ (15)

These error estimates do not include any uncertainties in production rates and scaling factors, which are difficult to quantify, but can be evaluated by using a range of input parameters.

Calculations with two nuclides

Equation 8 has three unknowns (t, $\epsilon$ and $\tau$). If two nuclides have been measured (with concentrations $N_1$ and $N_2$, say), only one value must be assumed in order to solve for the remaining two. By assuming zero erosion ($\epsilon$ = 0), CosmoCalc simultaneously calculates the exposure age and burial age (Section 5); by assuming steady-state erosion (t = $\infty$), the erosion rate and burial age are calculated; and by assuming zero-burial ($\tau$ = 0), the erosion rate and exposure age can be computed (Section 5).

Burial dating

If a rock surface gets buried by sediments or covered by ice, it is shielded from cosmic rays and the concentration of cosmogenic radionuclides decays with time. Such samples plot outside the steady-state erosion island of the banana plot, in the so-called field of ``complex exposure history'', a feature which is considered undesirable by most studies. Other studies, however, intentionally target complex exposure histories, using radionuclides to date pre-exposure and burial (e.g., Bierman et al., 1999; Fabel et al., 2002; Partridge et al., 2003). CosmoCalc calculates burial ages, either by assuming negligible erosion or steady state erosion ($\epsilon$ = 0 or t = $\infty$, respectively). It does not handle post-depositional nuclide production.

Burial - Exposure dating

If $\epsilon$ = 0, Equation 8 reduces to:

$$N = e^{-\lambda \tau} \frac{SP}{\lambda} \left( 1 - e^{- \lambda t} \right)$$ (16)

The easiest case of two-nuclide dating is that of simultaneously calculating exposure age (t) and burial age ($\tau$) with one radionuclide and one stable nuclide. Because the stable nuclide is not affected by burial, it can be used to calculate the pre-exposure age, using Equation 12. This age can then be used to calculate the burial age:

$$\tau = \frac{1}{\lambda}  ln\left( \frac{SP}{N\lambda}\left( 1 - e^{-\lambda t}\right) \right)$$ (17)

In the case of two radionuclides, CosmoCalc finds t by iteratively solving the following equation using Newton's method:

$$\lambda_2 ln\left( \frac{(SP)_1}{N_1\lambda_1}\left( 1 - e^{-\la... ...left( \frac{(SP)_2}{N_2\lambda_2}\left( 1 - e^{-\lambda_2 t}\right) \right) = 0$$ (18)

With $\lambda_1 > \lambda_2$. The solution is then plugged into Equation 17, using nuclide 1.

Burial - Erosion dating

Setting t = $\infty$ in Equation 8 yields the following system of non-linear equations for TCN concentrations $N_1$ and $N_2$:

$$\left\{ \begin{array}{l} f_1(\epsilon,\tau): N_1 = P_1 e^{- \la... ...S_{i,2} F_{i,2}}{\lambda_2 + \epsilon \rho / \Lambda_{i,2}} \end{array}\right.$$ (19)

These equations are easy to solve since the variables $\tau$ and $\epsilon$ are separated. If nuclide 1 has the shortest half-life (largest decay constant $\lambda$), the burial age is written as a function of the erosion rate $\epsilon$:

$$\tau = \frac{1}{\lambda_1} ln\left(\frac{P_1}{N_1} \sum_{i=0}^3 \frac{S_{i,1} F_{i,1}}{\lambda_1 + \epsilon \rho / \Lambda_{i,1}}\right)$$ (20)

The erosion rate is given implicitly by:

$$\lambda_2 ln\left(\frac{P_1}{N_1} \sum_{i=0}^3 \frac{S_{i,1} F... ... \frac{S_{i,2} F_{i,2}}{\lambda_2 + \epsilon \rho / \Lambda_{i,2}}\right) = 0$$ (21)

CosmoCalc solves Equation 21 for $\epsilon$ using Newton's method and then plugs this value into Equation 20. If $\lambda_2 < \lambda_1$, then $N_2$ is used instead of $N_1$ in Equation 20.

Age-erosion rate calculations

Assuming zero burial ($\tau$ = 0) yields the following system of equations $f_1$ and $f_2$:

$$\left\{ \begin{array}{l} f_1(\epsilon,t): N_1 = P_1 \sum_{i=0}^... ...lambda_2 + \epsilon \rho / \Lambda_{i,2} \right) t} \right) \end{array}\right.$$ (22)

It is impossible to solve these equations for exposure age (t) and erosion rate ($\epsilon$) separately. Instead, CosmoCalc implements the two-dimensional version of the Newton-Raphson algorithm:

$$\begin{bmatrix} \epsilon_{k+1} t_{k+1} \end{bmatrix} = \b... ...1} \begin{bmatrix} f_1(\epsilon_k,t_k) f_2(\epsilon_k,t_k) \end{bmatrix}$$ (23)

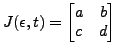With $J(\epsilon,t) = \begin{bmatrix}a&b c&d\end{bmatrix}$ the Jacobian matrix, which is also used for error propagation.

Error propagation

Error propagation is less straightforward in the two-dimensional case than in the single nuclide case (Section 5). The bijection from ($N_1$,$N_2$)-space to ($\epsilon$,t)-space is not orthogonal, particularly in the case of age-erosion dating (Section 5). For this reason, it is only possible to analytically compute upper bounds for $\sigma(\epsilon)$, $\sigma(\tau)$ and $\sigma$(t):

$$\begin{bmatrix} \sigma(x) \sigma(y) \end{bmatrix} \leq \... ...-1} \end{Vmatrix} \begin{bmatrix} \sigma(N_1) \sigma(N_2) \end{bmatrix}$$ (24)

with x and y placeholders for $\epsilon$ and t or $\tau$, respectively, and $\lVert \cdot \rVert$ the absolute values of the matrix $\left [ \cdot \right ]$. In the case of age-erosion dating, the confidence intervals for t and $\epsilon$ are very wide, often too wide to be useful. Therefore, it can be more productive to solve each quantity separately instead of simultaneously. Thus, using equations 11 and 13, it is possible to estimate minimum exposure ages and maximum erosion rates (e.g., Nishiizumi et al., 1991). However, for burial dating there is no choice and we must simultaneously solve for $\tau$ and $\epsilon$ or t.

In addition to Newton's method, CosmoCalc offers a second way of solving equations 19 and 22 by means of Monte Carlo simulation, implementing the Metropolis-Hastings algorithm (Metropolis et al., 1953; Tarantola, 2004). The Metropolis-Hastings algorithm is a so-called Bayesian MCMC (Markov Chain Monte Carlo) method. It not only finds the best solution to the system of non-linear equations, but actually explores the entire solution space. If the ``Metropolis'' option of the Age-Erosion function is selected, CosmoCalc generates 1000 ``acceptable'' solutions to Equation 19 or 22, where ``acceptable'' is defined by the bivariate normal likelihood of the forward-modeled TCN concentrations (Figure 3). The last 900 of these solutions are then ranked according to their likelihood. For a 95% confidence interval, those solutions with the lowest 5% likelihoods of the 900 results are discarded, leaving 855 values for $\epsilon$, t or $\tau$. The minimum and maximum values of these 855 numbers are the lower and upper bounds, respectively, of the simultaneous 95% confidence intervals. In contrast with the symmetric confidence intervals given by equation 24, the MCMC confidence limits are always greater than or equal to zero. However, as said before, the 95% confidence intervals can be very wide especially in the case of age-erosion dating.

Figure 3: Starting with a random guess (white star) for the erosion rate ($\epsilon$) and burial age ($\tau$), the Metropolis-Hastings algorithm quickly finds the optimal solution. It then continues to randomly sample the solution space defined by the measurement uncertainties. The white ellipse is the 2$\sigma$ confidence region, which corresponds to $\sim$90% of the bivariate ($\epsilon$,$\tau$) solution-space. The black area contains the last 90% of the 1000 accepted values generated by the algorithm. 95% of these 900 values are used to calculate the simultaneous confidence intervals for $\epsilon$ and $\tau$.

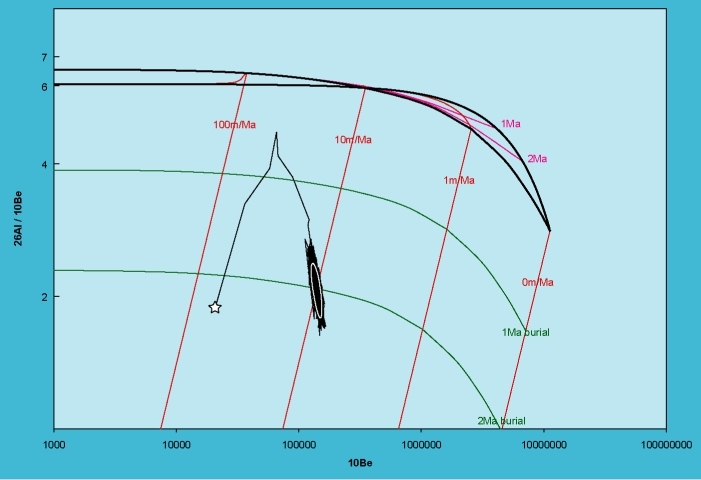
An a posteriori modification of the banana plots

Section 4 discussed the construction of $^{26}$Al-$^{10}$Be and $^{21}$Ne-$^{10}$Be banana plots. To plot samples from different field locations (with different latitude, elevation and shielding conditions) together on the same banana plot, it is necessary to scale the TCN concentrations to SLHL. In other words, each TCN concentration must be divided by an appropriate scaling factor, the so-called ``effective scaling factor'' $S_e$ (Equation 5):

$$S_e = \frac{N_{meas}}{N_{SLHL}}$$ (25)

With $N_{meas}$ the measured TCN concentration, and $N_{SLHL}$ the equivalent TCN concentration which would be measured had the sample been collected from SLHL. In the case of zero erosion, $N_{SLHL}$ = $N_{meas}$ / ( $S_p \times S_t \times S_s \times S_c$). This is no longer true when $\epsilon > 0$, because the relative contributions of neutron spallation, slow and fast muons change below the surface. This is the ``fractionation'' effect that was discussed in Section 4 and quantified by Equation 10. For example, consider the case of two high latitude, high elevation samples, one with negligible erosion ($\epsilon$=0) and one with non-zero erosion ( $\epsilon > 0$). Because the relative importance of neutron spallation increases with decreasing erosion rate, and neutrons are more important (relative to muons) at higher elevations, $S_e$ will be greater for the zero-erosion than for the non-zero erosion case. CosmoCalc first solves Equation 19 or 22 for $\epsilon$ and $\tau$ or t, whichever fits the measured TCN concentrations best. Plugging these solutions into Equation 4 yields the equivalent TCN concentration at SLHL. $S_e$ is then given by Equation 25.