CONCLUSIONS

It was not the purpose of this paper to claim that discriminant analysis or discrimination diagrams are either bad or obsolete. It merely suggests a completely different statistical approach to tectonic classification by rock geochemistry. Classification trees are presented as a simple yet powerful way to classify basaltic rocks of unknown tectonic affinity. Some of the strengths of the method are:

• Classification trees approximate the feature space by a piecewise constant function. This non-parametric approach avoids the statistical quagmire of discriminant analysis on compositional data (e.g., Aitchison, 1986; Woronow and Love, 1990).
• Classification trees are insensitive to outliers. In other words, if some of the training data were misidentified or accidentally very inaccurate (e.g., misplaced decimal point), trees remain almost unaffected.
• They can be used for the classification of highly multivariate data, while preserving the possibility of a simple, two-dimensional visualization. Therefore, trees are extremely easy to use. The trees presented in this paper were based on a database of moderate size (756 analyses). If a much larger database were compiled, the trees would grow and their discriminative power increase, but they would still be easy to interpret. It should also be easy to extend the trees given in this paper to more tectonic affinities, such as active continental margins, continental within-plate basalts, or different lithologies, simply by adding data to the training-set. In principle, there is no upper limit to the number of ``class labels'' that the method can discriminate, provided enough training data are available.
• Trees do not discriminate according to some complicated decision boundary (e.g., multivariate discriminant analysis) or a black box process (e.g., neural networks), but split the data space up one variable at the time, in decreasing order of significance. Therefore, the split variables have geochemical significance. For example, if TiO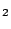$_2$ and Sr contribute 87% of the discriminative power, there likely is a real geochemical mechanism that causes this to be so.
• Although the trees presented in this paper were built from as many as 51 different variables, we can still use them if some of these variables were not measured for the unknown sample that we want to classify. This can be done with the surrogate split variables of Tables 1 and 2.
• A rough idea can be had of the statistical uncertainty of the classification by looking at the purity of the terminal nodes. For examples, see samples GR 181b and 56c of Section 4.2. This is not possible for discrimination diagrams because the decision boundaries of the latter are drawn as hard lines, and not as the ``fuzzy'' zones which they really are.

On the other hand, trees are not perfect, and also have a few problems:

• Classification trees are biased because the piecewise constant approximation which they implement is an oversimplification of the feature space. Increasing the size of the training dataset will alleviate this problem. Alternatively, we could also allow linear combination splits instead of only splits on a single variable, but this would hurt interpretability.
• Trees also suffer from large variance. In other words, they are unstable. A different set of training data could result in very different looking trees. This somewhat limits the interpretability of the split variables, which was hailed before. More importantly, small errors in one of the split variables of the unknown dataset are propagated down to all of the splits below it. ``Bagging'' is a way to solve these problems by collecting a large number of ``bootstrap samples'' of the training data, and building a large number of trees from them (Hastie et al., 2001). The unknown data are then sent through all these trees and the results averaged. This provides a more robust classification algorithm, but again at the expense of interpretability, because bagged trees can no longer be easily plotted as a simple two-dimensional graph.
• One of the properties of many data mining algorithms, including classification trees, is the ``garbage in, garbage out'' principle. There is no field of ``ambiguous'' tectonic affinity, which is effectively the output of geochemical compositions that plot ``out of bounds'' on traditional discrimination diagrams (e.g., Figure 6 and Table 3). Any rock will be classified as either IAB, MORB or OIB, also when it really is a continental basalt, granite or even sandstone! Therefore, one might treat compositions that plot far outside the decision boundaries of the traditional discrimination diagrams with extra caution.

Most importantly, as was illustrated by the examples of Section 3, no classification method based solely on geochemical data will ever be able to perfectly determine the tectonic affinity of basaltic rocks (or other rocks for that matter) simply because there is a lot of actual overlap between the geochemistry of the different tectonic settings. Notably IABs have a much wider range of compositions than either MORBs or OIBs. Therefore, geochemical classification should never be the only basis for determining tectonic affinity. This is especially the case for rocks that have undergone alteration. In such cases, mobile elements such as Sr, which have great discriminative power, cannot be used. If in addition to this, some other features have not been measured (such as isotope ratios and rare earths in some of the samples of Table 9), then one might not be able to put much faith in the classification.