next up previous
Next: A Tree of HFS Up: APPLICATION TO THE TECTONIC Previous: APPLICATION TO THE TECTONIC


A Tree Using Major, Minor and Trace Elements and Isotope Ratios

In a first approach, all 51 features were used for the tree construction, including relatively mobile elements such as CaO and Na$_2$O. Therefore, the resulting tree should only be used on fresh samples of basalt. The largest possible tree (T$_0$) has 51 splits, and actually uses only 23 of the 51 selected features. These are: SiO$_2$, TiO$_2$, CaO, Fe$_2$O$_3$, MgO, K$_2$O, La, Pr, Nd, Sm, Gd, Tb, Yb, Lu, V, Ni, Rb, Sr, Y, Hf, Th, $^{87}$Sr/$^{86}$Sr and $^{206}$Pb/$^{204}$Pb. The remaining 28 features apparently did not contain enough discriminative power. As discussed in Section 2, T$_0$ is not the best possible tree. 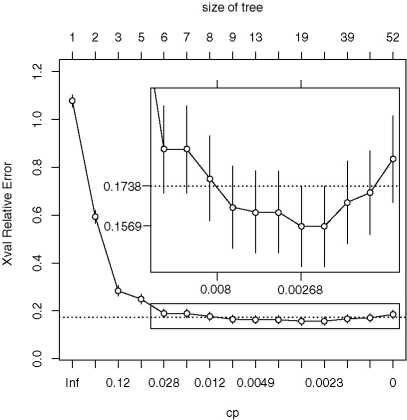A plot of relative cross-validation misclassification risk versus tree size shows a minimum at 18 splits (Figure 3). 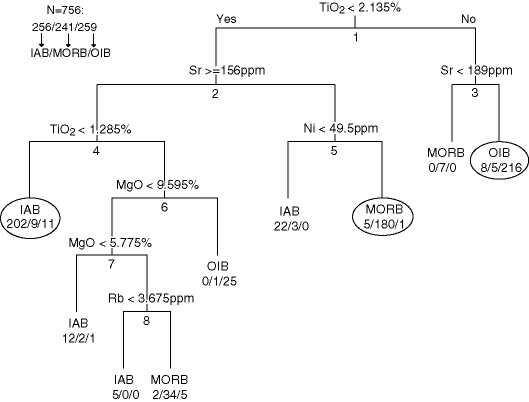Using the 1-SE rule then puts the optimal tree size at 8 splits (Figure 3). The resulting, optimally pruned tree is shown in Figure 4.

Figure 3: Choosing the optimal tree size. The y-axis shows the ten-fold cross-validation error, relative to the misclassification risk of the root node (=497/756). The x-axes show the size of the tree (i.e., the number of nodes) and the complexity parameter (cp). The first two splits account for 87% of the discriminative power. The inset shows a magnification of the boxed part of the curve, illustrating the 1-SE rule.
Image W3441-fig3

Figure 4: The optimal classification tree, based on a training set of 756 geochemical analyses of at most 51 elements and isotopic ratios. The ``heaviest'' terminal nodes are encircled.
Image W3441-fig4

The classification by the optimal tree is remarkably successful. No less than 79% of all the training data correctly fall in just three terminal nodes (encircled in Figure 4). Only 7% of the training data were misclassified, while the ten-fold cross-validation error is about 11%, corresponding to a success-rate of 89%. In other words, the probability that a sample of unknown tectonic affinity will be classified correctly is 89%. The first two splits (on TiO$_2$ and Sr) account for 87% of the discriminative power (Figure 3). In a way, this can be seen as a justification of the use of these elements in popular discrimination diagrams such as the Ti-Zr-Sr diagram (Pearce and Cann, 1973). An analysis of TiO$_2$ and Sr alone already gives a pretty reliable classification. For example, if TiO$_2$$\geq$2.135%, the tree tells us there is a 91% chance that the rock has an OIB affinity. 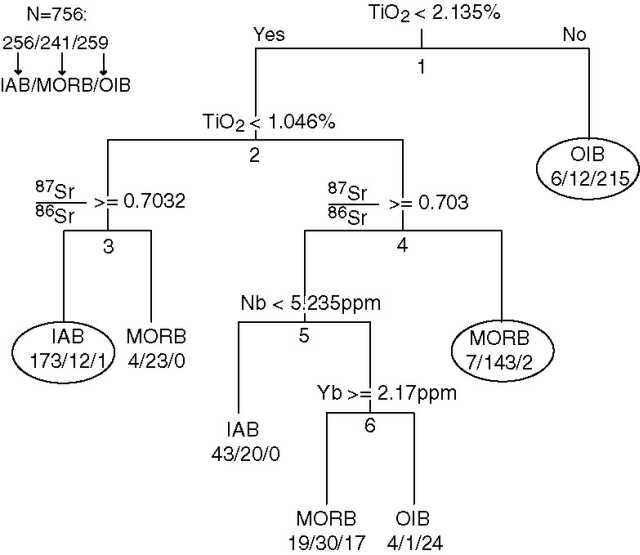Likewise, 87% of the training data with TiO$_2$$<$2.135% and Sr$<$156ppm are MORBs. For further discrimination, additional elements can be used, which inevitably increases the chance of missing variables. However, as discussed before, classification trees elegantly resolve this problem with surrogate split variables, which are shown in Table 1.


Table 1: Primary and surrogate splits for the nodes of Figure 4. The nodes without surrogates do not have any alternative variables that do better than a ``go with the majority'' decision (given by the second column of the table). Split number 8 has only one worthwhile surrogate.
split number IAB/MORB/OIB primary split surrogate 1 surrogate 2
1 256/241/259 TiO$_2$$<$2.135% P$_2$O$_5$$<$0.269% Zr$<$169.5ppm
2 248/229/43 Sr$\geq$156ppm K$_2$O$\geq$0.275% Rb$\geq$3.965ppm
3 8/12/216 Sr$<$189ppm - -
4 221/46/42 TiO$_2$$<$1.285% Al$_2$O$_3$$\geq$15.035% SiO$_2$$\geq$46.335%
5 27/183/1 Ni$<$49.5ppm Cr$<$82ppm TiO$_2$$<$0.71%
6 19/37/31 MgO$<$9.595% SiO$_2$$\geq$46.605% Al$_2$O$_3$$\geq$13.945%
7 19/36/6 MgO$<$5.775% Al$_2$O$_3$$\geq$17.03% CaO$<$10.02%
8 7/34/5 Rb$<$3.675ppm Na$_2$O$\geq$4% -


Figure 5: The optimal classification tree using only HFS cations and isotopic ratios. The encircled terminal nodes contain the bulk of the training data.
Image W3441-fig5


Table 2: Surrogate splits for the HFS tree shown in Figure 5.
split number IAB/MORB/OIB primary split surrogate 1 surrogate 2
1 256/241/259 TiO$_2$$<$2.135% Zr$<$169.5ppm -
2 250/229/44 TiO$_2$$<$1.0455% Zr$<$75.5ppm Y$<$22.9ppm
3 177/35/1 $^{87}$Sr/$^{86}$Sr$\geq$0.703175 - -
4 73/194/43 $^{87}$Sr/$^{86}$Sr$\geq$0.703003 $^{143}$Nd/$^{144}$Nd$<$0.5130585 Nd$\geq$12.785ppm
5 66/51/41 Nb$<$5.235ppm TiO$_2$$<$1.565% Zr$<$100.5ppm
6 23/31/41 Yb$\geq$2.17ppm Lu$\geq$0.325ppm Sm$\geq$3.705ppm


next up previous
Next: A Tree of HFS Up: APPLICATION TO THE TECTONIC Previous: APPLICATION TO THE TECTONIC
Pieter Vermeesch 2005-12-14