Generalized equations for (U-Th-Sm)/He dating

For reasons given in the Introduction, $^{147}$Sm is often neglected in helium thermochronometry. However, in rare cases it does happen that apatite contains high abundances of Sm, affecting the helium age on the percent level. This section will explain how to add a fourth radioactive parent to the methods described above. The exact age equation (equation 2) and the present-day helium production rate (equation 4) can easily be generalized to include Sm:

$$\begin{split}[He]= \left( 8\frac{137.88}{138.88}\left(e^{\lam... ...[Th] + 0.1499\left(e^{\lambda_{147}t}-1\right)[Sm] \end{split}$$ (18)

and

$$P = \left( 8\frac{137.88}{138.88}\lambda_{238} + \frac{7}{138.88}\lambda_{235} \right) [U]+ 6\lambda_{232}[Th] + 0.1499\lambda_{147}[Sm]$$ (19)

With $\lambda_{147}$ the decay constant of $^{147}$Sm and all other parameters as in equations 2 and 4. Using equation 19, calculating an isochron age for (U-Th-Sm)/He proceeds in exactly the same way as for the ordinary (U-Th)/He method, and the same is true for the pooled age. Calculating (U-Th-Sm)/He central ages is also very similar, although the equations are a bit longer. In addition to V$_i$ and W$_i$ (equation 11), we define a third logratio variable X$_i$ (1$\leq$i$\leq$n):

$$V_i = ln\left(\frac{[U_i]}{[He_i]}\right),~ W_i = ln\left(\frac{[Th_i]}{[He_i]}\right),~ X_i = ln\left(\frac{[Sm_i]}{[He_i]}\right)$$ (20)

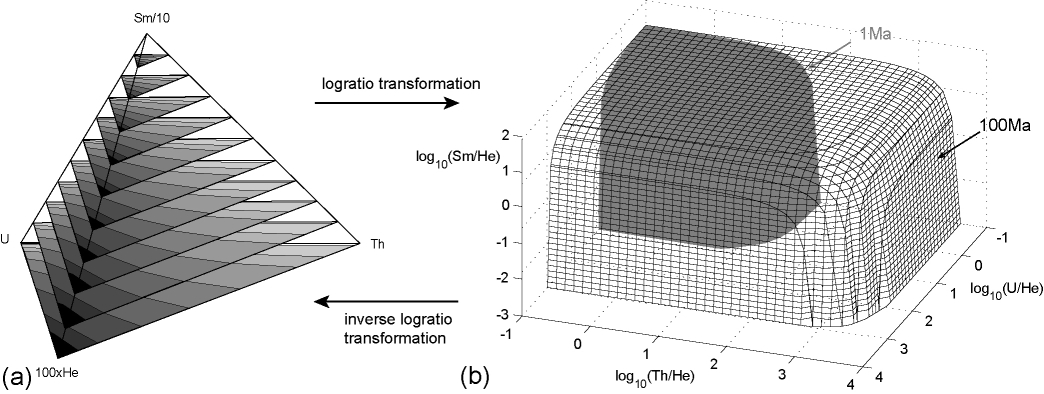
Because there are three instead of two logratio variables, the (U-Th-Sm)/He age equation cannot be visualized on a straightforward bivariate diagram, but forms a set of hypersurfaces in trivariate logratio-space (Figure 7). Likewise, (U-Th-Sm)/He data do not form a ternary, but a tetrahedral system in compositional dataspace (Figure 7). Generalizing the (co)variances of equation 12:

$$\begin{split} & \hat{\sigma}_{V_i}^2 = \left(\frac{\sigma_{U... ..._i,X_i} =\left(\frac{\sigma_{He_i}}{He_i}\right)^2 \end{split}$$ (21)

Calculating the arithmetic logratio-means:

$$\overline{V} = \frac{1}{n} \sum_{i=1}^n V_i,~ \overline{W} = \frac{1}{n} \sum_{i=1}^n W_i,~ \overline{X} = \frac{1}{n} \sum_{i=1}^n X_i$$ (22)

The (co-)variances of the logratio-means, propagating only the internal error:

$$\begin{split} & \hat{\sigma}_{\overline{V}}^2 = \frac{1}{n^2... ...ine{X}} = \frac{1}{n^2} \sum_{i=1}^n cov_{W_i,X_i} \end{split}$$ (23)

The (co-)variances of the logratio-means, propagating the external error:

$$\begin{split} \hat{\sigma}_{\overline{V}}^2 = \frac{\sum_{i=... ... (W_i - \overline{W})(X_i - \overline{X})}{n(n-1)} \end{split}$$ (24)

The inverse logratio-transformation:

$$\begin{split} & \overline{[U]} = \frac{e^{\overline{V}}}{e^{... ...\overline{V}}+e^{\overline{W}}+e^{\overline{X}}+1} \end{split}$$ (25)

Finally, calculating the standard error propagation of the geometric mean compositions:

$$\left( \begin{array}{c} \hat{\sigma}_{\overline{U}}^2 \\ \hat... ...V},\overline{X}} \\ cov_{\overline{W},\overline{X}} \\ \end{array} \right)$$ (26)

with

$$a = \frac{e^{\overline{V}}(e^{\overline{W}}+e^{\overline{X}}+1)} {(e^{\overline{V}}+e^{\overline{W}}+e^{\overline{X}}+1)^2} b = \frac{-e^{\overline{V}+\overline{W}}} {(e^{\overline{V}}+e^{\overline{W}}+e^{\overline{X}}+1)^2}$$

$$c = \frac{-e^{\overline{V}+\overline{X}}} {(e^{\overline{V}}+e^{\overline{W}}+e^{\overline{X}}+1)^2} d = \frac{e^{\overline{W}}(e^{\overline{V}}+e^{\overline{X}}+1)} {(e^{\overline{V}}+e^{\overline{W}}+e^{\overline{X}}+1)^2}$$

$$e = \frac{-e^{\overline{W}+\overline{X}}} {(e^{\overline{V}}+e^{\overline{W}}+e^{\overline{X}}+1)^2} f = \frac{e^{\overline{X}}(e^{\overline{V}}+e^{\overline{W}}+1)} {(e^{\overline{V}}+e^{\overline{W}}+e^{\overline{X}}+1)^2}$$

$$g = \frac{-e^{\overline{V}}} {(e^{\overline{V}}+e^{\overline{W}}+e^{\overline{X}}+1)^2} h = \frac{-e^{\overline{W}}} {(e^{\overline{V}}+e^{\overline{W}}+e^{\overline{X}}+1)^2}$$

$$i = \frac{-e^{\overline{X}}} {(e^{\overline{V}}+e^{\overline{W}}+e^{\overline{X}}+1)^2} ~$$

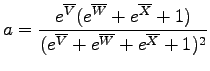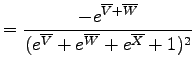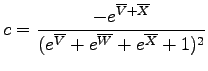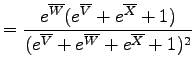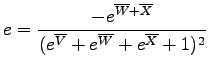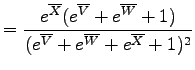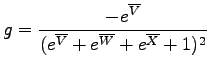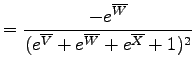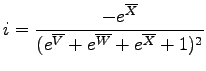An example of a well-behaved (U-Th-Sm)/He dataset from the Fish Lake Valley apatite standard (provided by Prof. Daniel Stockli, University of Kansas) is given in the web-calculator ( http://pvermees.andropov.org/central). The arithmetic mean of 28 single-grain ages is 6.36 $\pm$ 0.11 Ma, the pooled age 6.43 $\pm$ 0.21 Ma, the isochron ages 6.44 $\pm$ 0.67 Ma (with an intercept of -0.005 $\pm$ 0.056 fmol/$\mu$g, and the central age 6.41 $\pm$ 0.14 Ma. Note that the central age is older and not younger than the arithmetic mean age. This indicates that random variations exceed the very small systematic difference between the arithmetic and geometric mean compositions. However, the central age probably still is more accurate than the arithmetic mean age because it is less sensitive to outliers.

Figure 7: The logratio-transformation can easily be generalized to the case of 3 radioactive parents but this precludes a straightforward visualization on a two-dimensional diagram. (a) the (U-Th-Sm)/He age equation in compositional dataspace. (b) two hypersurfaces representing two ages in logratio-space.