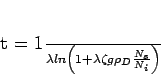Taking into account unequal measurement uncertainties

In the toy example discussed before, all measurements had equal measurement uncertainties. This is seldom the case in real world applications, particularly when fission track dating is involved. Most importantly, AFT age uncertainties are a sensitive function of the number of spontaneous fission tracks. Young grains have fewer spontaneous tracks than older grains of similar U-concentration. This results in widely variable measurement uncertainties ranging from a few percent for old, U-rich grains to more than 100% for U-poor grains containing little or no fission tracks. As explained in the previous section, measurement uncertainties are incorporated in the predicted, rather than the observed CAD. The problem of unequal measurement uncertainties can be mitigated by using Brandon's [1996] logarithmic ``z-transformation'' (Equation 3). Although this is a valid approach, we will use the regular age-equation in the following.

The sand and gravel samples discussed in this paper were dated with the external detector method [Hurford and Green, 1983]. The age equation for this method is:

$$t = \frac{1}{\lambda}ln\left( 1+ \lambda \zeta g \rho_D \frac{N_s}{N_i} \right)$$ (7)

with all variables as in Equation 3. Using the external detector method, fission track ages (t) are roughly proportional to the ratio of the expected number of spontaneous tracks (N$_s$) in the mineral grain to the expected number of tracks induced by neutron irradiation (N$_i$): t $\propto$ N$_s$/N$_i$. However, if N$_s$ and/or N$_i$ are small numbers ($<$10), then the observed ratio of spontaneous ($\hat{N}_s$) to induced ($\hat{N}_i$) tracks can potentially be very different. For example, if N$_s$=2, there is 14% chance that $\hat{N}_s$=0, resulting in an AFT age $\hat{t}\propto\hat{N}_s/\hat{N}_i$ = 0. Assuming that there is no systematic correlation between N$_i$ and t, the effect of Poisson-distributed counting statistics on the CAD can be modeled as follows:

1. Consider a probability distribution of AFT ages, for example k = 1000 numbers drawn from the cumulative hypsometry.
2. For each of these ages t$_j$ (1$\leq$j$\leq$k), randomly select a N$_i$ value ($N_i^j$, say) from the database of measurements (Tables 5 and 6 of the auxiliary material).
3. Compute the expected number of fission tracks ($N_s^j$) corresponding to t$_j$ and N$_i^j$ by rearranging Equation 7:

   
   

   $$N_s^j = \frac{N_i^j}{\lambda \zeta g \rho_D} \left( e^{\lambda t_j} - 1 \right)$$ (8)

   
   

4. Generate random replicates $N_s^{j*}$ of $N_s^j$ and $N_i^{j*}$ of $N_i^j$ by sampling at random from a Poisson distribution:

   
   

   $$N_s^{j*} \sim Poiss(N_s^j)\mbox{, and }N_i^{j*} \sim Poiss(N_i^j)$$ (9)

   
   

5. Plug $N_s^{j*}$, $\zeta^j$ and N$_i^{j*}$ into Equation 7. This yields a replicate age t$_j^*$. Doing this for all k errorless AFT ages from the expected CAD yields a new CAD (the ``predicted CAD'') that does take into account Poisson-distributed measurement uncertainties. Note that this CAD effectively follows the definition of Ruhl and Hodges' [2005] CSPDF$_{t*m}$ curve.