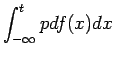 |
(5) | ||
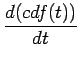 |
(6) |
The probability density function (PDF) is intimately linked to the cumulative density function (CDF). The relationship between PDF and CDF is:
PDF and CDF are standard statistical terms. In the nomenclature of
Ruhl and Hodges [2005], the specific case of a Gaussian kernel
density estimator with ![]() = 1 is named SPDF, and the
corresponding CDF is named the Cumulative Synoptic Probability Density
Function (CSPDF). Thus, the CSPDF is defined by using SPDF instead of
PDF in Equation 5. Although SPDF and CSPDF are
interchangeable from a statistical point of view, the CSPDF has
recently gained considerable popularity for two reasons. First, the
cumulative distribution has intuitive significance, as its shape
mimics the shape of the the cumulative hypsometry (modulated by the
age-elevation curve). A second advantage of cumulative plots is the
ease of comparing different datasets by using the Kolmogorov-Smirnov
(K-S) goodness-of-fit test. The K-S test determines if the maximum
vertical distance between two cumulative distributions can be
explained by random sampling effects alone. As illustrated by Amidon et al. [2005], using the CSPDF in combination with the K-S
test is a useful tool for comparing two detrital datasets. However, we
will next see that the CSPDF should not be used for the purpose
of comparing a detrital age distribution with hypsometric predictions.
= 1 is named SPDF, and the
corresponding CDF is named the Cumulative Synoptic Probability Density
Function (CSPDF). Thus, the CSPDF is defined by using SPDF instead of
PDF in Equation 5. Although SPDF and CSPDF are
interchangeable from a statistical point of view, the CSPDF has
recently gained considerable popularity for two reasons. First, the
cumulative distribution has intuitive significance, as its shape
mimics the shape of the the cumulative hypsometry (modulated by the
age-elevation curve). A second advantage of cumulative plots is the
ease of comparing different datasets by using the Kolmogorov-Smirnov
(K-S) goodness-of-fit test. The K-S test determines if the maximum
vertical distance between two cumulative distributions can be
explained by random sampling effects alone. As illustrated by Amidon et al. [2005], using the CSPDF in combination with the K-S
test is a useful tool for comparing two detrital datasets. However, we
will next see that the CSPDF should not be used for the purpose
of comparing a detrital age distribution with hypsometric predictions.
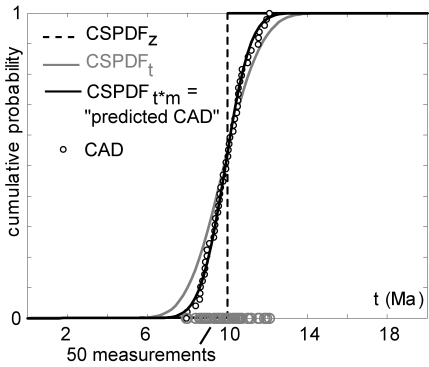
Revisiting the toy example of a ``diving board'' hypsometry, the CDF
of the true ages is a step-function at t![]() = 10Ma (Figure
4). The theoretical CDF of the measured ages
(
= 10Ma (Figure
4). The theoretical CDF of the measured ages
(![]() CSPDF
CSPDF![]() curve of Ruhl and Hodges, 2005) is the
cumulative normal distribution with mean 10Ma and standard deviation
1Ma (red curve on Figure 4). In contrast, the
cumulative kernel density estimator CSPDF
curve of Ruhl and Hodges, 2005) is the
cumulative normal distribution with mean 10Ma and standard deviation
1Ma (red curve on Figure 4). In contrast, the
cumulative kernel density estimator CSPDF![]() (gray curve on Figure
4) is the cumulative normal distribution with mean
10Ma and standard deviation
(gray curve on Figure
4) is the cumulative normal distribution with mean
10Ma and standard deviation ![]() Ma. Thus, CSPDF
Ma. Thus, CSPDF![]() is not a
good estimator of CSPDF
is not a
good estimator of CSPDF![]() , for the same reason why SPDF
, for the same reason why SPDF![]() is
not a good estimator of SPDF
is
not a good estimator of SPDF![]() (Figure
3). In other words, the CSPDF is not a good
tool for comparing detrital datasets with hypsometric predictions,
which is exactly the goal of this paper. Fortunately, the misfit
caused by the ``double smoothing'' of CSPDF
(Figure
3). In other words, the CSPDF is not a good
tool for comparing detrital datasets with hypsometric predictions,
which is exactly the goal of this paper. Fortunately, the misfit
caused by the ``double smoothing'' of CSPDF![]() does not greatly
affect the conclusions of Ruhl and Hodges [2005] and Stock
et al. [2006], because the analytical uncertainties of their
does not greatly
affect the conclusions of Ruhl and Hodges [2005] and Stock
et al. [2006], because the analytical uncertainties of their
![]() Ar/
Ar/![]() Ar and (U-Th)/He data are relatively small. The
situation would be worse for the less precise AFT data presented here.
Ar and (U-Th)/He data are relatively small. The
situation would be worse for the less precise AFT data presented here.
[h]
|
The CSPDF-method can be ``fixed'' by smoothing the CSPDF![]() a
second time. In practice, CSPDF
a
second time. In practice, CSPDF![]() can be constructed by
collecting a large number of synthetic ``measurements'' from the
hypsometry and adding a synthetic measurement error to them. The
second smoothing step would then involve stacking a bell curve on top
of each of the sythetic measurements, as in Equation 2.
Instead of this cumbersome ``fix'', the Cumulative Age Distribution
(CAD) is introduced as a simpler alternative to the CSPDF method.
can be constructed by
collecting a large number of synthetic ``measurements'' from the
hypsometry and adding a synthetic measurement error to them. The
second smoothing step would then involve stacking a bell curve on top
of each of the sythetic measurements, as in Equation 2.
Instead of this cumbersome ``fix'', the Cumulative Age Distribution
(CAD) is introduced as a simpler alternative to the CSPDF method.