How many grains are needed for a provenance study?
The general equation for the calculation of the probability p that at least one of M fractions >= f of the population is missed by all k grains of a sample is:
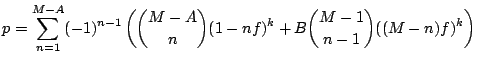 |
(1) |
Without specifying the number of fractions, the worst case probability pmax becomes:
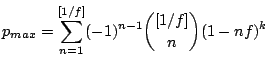 |
(2) |
For the following calculators to work, JavaScript must be enabled in your web browser.
Calculating k as a function of the desired p and f:
Example: to reduce the chance that at least one fraction f >= 0.05 has been missed to less than p = 5%, k = 117 grains have to be dated.Calculating fact for a given p and k:
Example: if k = 60 grains have been dated, the fraction that we know with (100-p) = 95% certainty not to have missed, is fact = 0.086Calculating pmax as a function of k and f:
Example: when k = 60 grains are dated of a uniformly distributed population, the chance that at least one fraction f >= 0.05 has been missed is pmax= 64%.Calculating Mopt for a given p, f and k:
Example: if we want to reduce the chance that at least one fraction f >= 0.05 was missed of a uniform population to less than p = 5%, and we have dated k = 100 grains, then we can only use Mopt = 9 bins in the age-histogram.